Мы настоятельно рекомендуем при написании научных публикаций, диссертаций и проведении маркетинговых исследований обращаться за проведением статистических исследований к нашим специалистам. Статистический методы имеют массу ограничений и особенностей интерпретации. Ценой ошибки может стать репутация вашего научного труда или эффективность вашего исследования. Мы сделаем для вас качественные статистические исследования для диссертаций. Публикации нашего сайта из цикла «Статистика» служат лишь для цели разъяснения вам отдельных нюансов и особенностей статистических методов.

Метод ближайших соседей широко применим для классификации объектов и интуитивно достаточно понятен. Его логика состоит в следующем: изучаемый объект мы отнесем к тому классу, к какому классу относится большинство ближайших «соседей» данного объекта. Например, пациента мы отнесем в ту группу, к которой относятся пациенты со схожими показателями анализов. Товар мы отнесем к той категории, к которой относятся товары со схожими характеристиками.

Суть метода ближайших соседей

Определять ближайших соседей в данной ситуации можно с помощью разных метрик. Чаще всего употребляют всем знакомое эвклидово расстояние, либо манхэттэнское расстояние, вычисляемое как сумму модулей разностей значений каждого независимого показателя. Все зависит от контекста решаемой задачи. Казалось бы, что метод должен работать и давать точные прогнозы классификации объектов везде и всегда. Именно поэтому его так часто применяют ученые или, например, маркетологи. Однако на самом деле его применение весьма ограничено и допустимо далеко не всегда. Именно об ограничениях его применимости мы и поговорим в этой статье, чтобы помочь вам избежать досадных ошибок.

Нестабильность метода ближайших соседей

Первый и очевидный минус метода ближайших соседей состоит, конечно же, в его нестабильности. Стоит независимому показателю чуть-чуть поменяться, как у изучаемого объекта может поменяться большая часть ближайших соседей, а значит, и предсказываемая категория.

Второй проблемой метода является правильный выбор количества рассматриваемых ближайших соседей. Ведь можно осуществлять классификацию по 3 ближайшим соседям, а можно по 10 или 15. При этом многим исследователям кажется, что наиболее точный результат может дать классификация объекта по 1 ближайшему соседу. Такой подход может дать массу ошибок классификации, особенно для тех объектов, которые находятся на границе классов.

Метод ближайших соседей при большом количестве независимых показателей

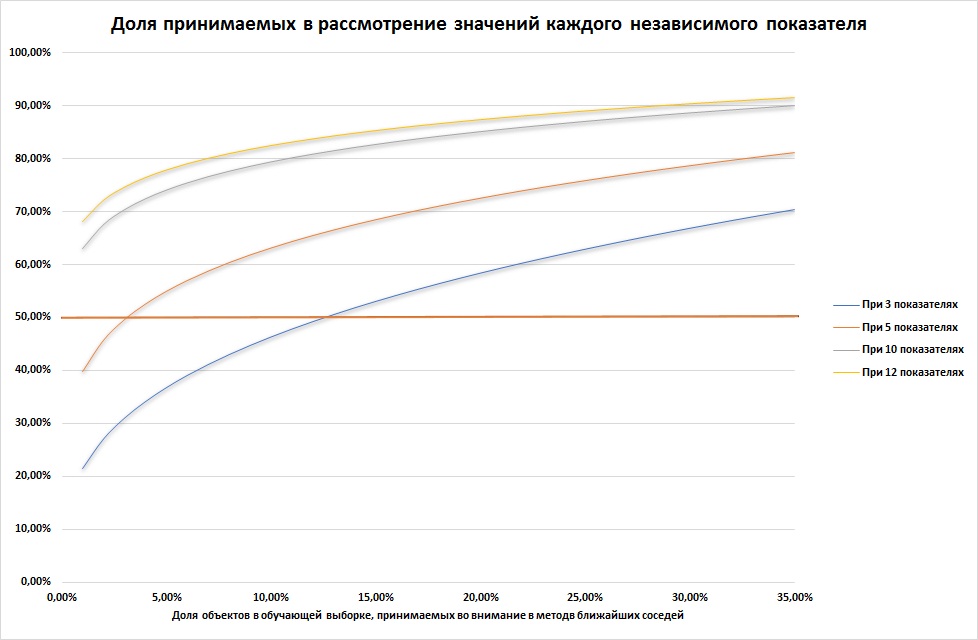
Поиск оптимальной величины k превращается в настоящую проблему при росте количества независимых показателей. Представим себе, что данные обучающей выборки ограничены некоторым гиперкубом (это многомерная фигура, каждая сторона которой ограничена возможным минимальным и максимальным значением одного независимого показателя обучающей выборки). Поставим перед собой цель выделить в нем меньший гиперкуб, в который войдет некоторая доля a элементов обучающей выборки. Очевидно, что сторона такого куба составит следующую долю от стороны исходного гиперкуба: e(a,p) = a^1/p, где p — количество независимых показателей, то есть количество измерений нашего гиперкуба.

Учитывая, что a — величина, меньшая 1, а p — целое число, с ростом a или p доля стороны e растет и быстро приближается к 1.  Например, e(5%,10) = 74%, e(15%,10) = 83%, e(5%,12) = 78%, e(15%,12) = 85%. То есть фактически, для того, чтобы изучить 5% долю соседей, нам нужно реально включить в рассмотрение 74% значений каждого из 10 независимых показателей, то есть большую их часть. Даже снижение a до 1% не дает существенных послаблений. А это означает, что решение о том, к какому классу принадлежит объект нам приходится принимать, основываясь на почти всех значениях, которые способы принимать независимые показатели. Как видим, если независимых показателей становится более 5, метод становится едва ли применимым.

Невозможность решения задачи классификации методом ближайших соседей для равномерно распределенных многомерных величин

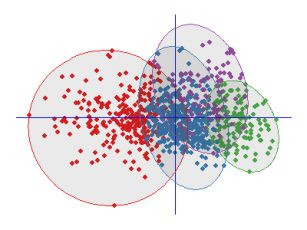
Другая проблема возникает, если данные обучающей выборки равномерно распределены в некотором объеме. Такие выборки в реальной практике не так редки. Оказывается, что в этой ситуации большинство значений показателей объектов из обучающей выборки будут сконцентрированы ближе к границе этого объема. Например, предположим, что данные равномерно распределены внутри p-мерного шара с центром в начале координат и радиусом r. Оценим медиану расстояния от начала координат до ближайшей точки обучающей выборки.

Объем такого шара пропорционален r^p. Если внутри данного шара построить меньший шар с центром в начале координат и радиусом kr, где k — некоторая доля, то вероятность того, что точка обучающей выборки не попала в этот шар составляет: (r^p-(kr)^p)/r^p.

Тогда вероятность, что все точки выборки не попали в этот шар составит (1-k^p)^N, где N — количество точек в обучающей выборке. Тогда искомое k вычисляется из расчета, что данная вероятность равна 50%:

k = (1-(0.5)^1/N)^1/p.

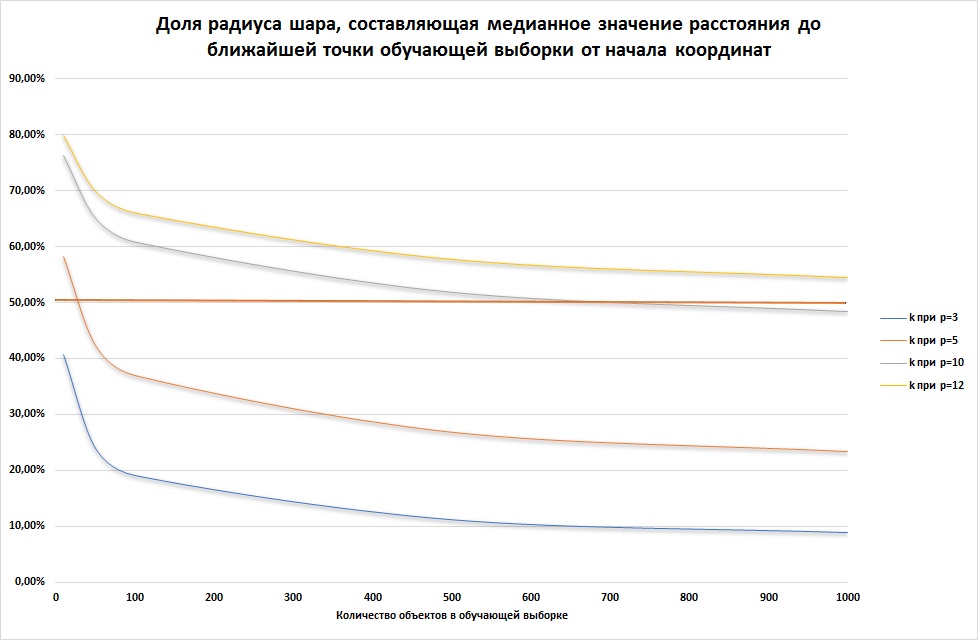
Как видим, при количестве независимых показателей более 5 и размере обучающей выборки менее 1 000, точки обучающей выборки концентрируются ближе к границе шара. Это означает, что задача по поиску значений классификации для точек ближе к центру шара становится задачей экстраполяции, решить которую с высокой точностью не представляется возможным.

В следующих статьях мы продолжим изучение вопроса о применимости данного метода.

Если же вам для диссертации или иной научной работы необходимо профессионально решить задачу классификации объектов (например, пациентов в зависимости от показателей крови по диагнозу) или регрессионную задачу, мы с радостью выполним для вас эту работу. Наши специалисты уже много лет оказывают услуги вузам по статистическим расчетам для диссертаций.

В этой и других статьях цикла использованы материалы книги Trevor Hastie, Robert Tibshirani, Jerome Friedman «The elements of statistical learning»